AI won’t replace humans
Artificial Intelligence, or AI for short, learns to discover patterns in data independently through sophisticated algorithms and powerful computing. This process, also called machine learning, allows computers to learn from data. While artificial intelligence is undeniably impressive, it is not magical, and it won’t replace humans anytime soon. However, concerns exist about the possibility of AI eventually surpassing human control, acting unpredictably, or imposing its will. To address this, regulations and ethical guidelines worldwide emphasize the importance of keeping AI systems controllable, with humans serving as supervisors. In both business and government, artificial intelligence is now widely used, though its success varies. This article explores the definition of AI, how it works, its models, and its applications, along with its advantages. It also discusses the different types of intelligence and the potential risks or accidents AI can cause. Finally, it touches on legislation, ethics, and sustainability in the context of AI.
What is artificial intelligence and what does AI mean?
There are many definitions of artificial intelligence (AI) in circulation, but we use the most concise and understandable one. In essence, it involves helping computers develop “learning capabilities” by exposing them to large amounts of data, which they analyze thoroughly using algorithms. We define artificial intelligence as follows:
Artificial intelligence learns to independently discover patterns and relationships in data through specific algorithms and unprecedented computing power.
Unlike traditional programs, AI cannot be programmed in the conventional sense – it essentially programs itself. In other words, it is fundamentally self-learning. This is the key difference from traditional programming, where a developer must anticipate and code for all possible scenarios. The self-learning nature is what truly defines artificial intelligence and gives it purpose. At its core, however, it is simply the automation of analyzing large or complex datasets.
There are two primary domains where artificial intelligence adds significant value:
- Thinking, learning, and deciding: The goal is automatic classification, clustering, event prediction, planning, problem-solving, and, if desired, even making decisions independently.
- Acting, tuning, and creating: AI in this domain is applied to robotics, autonomous vehicles, automated text generation, art creation, 3D printing, and translation.
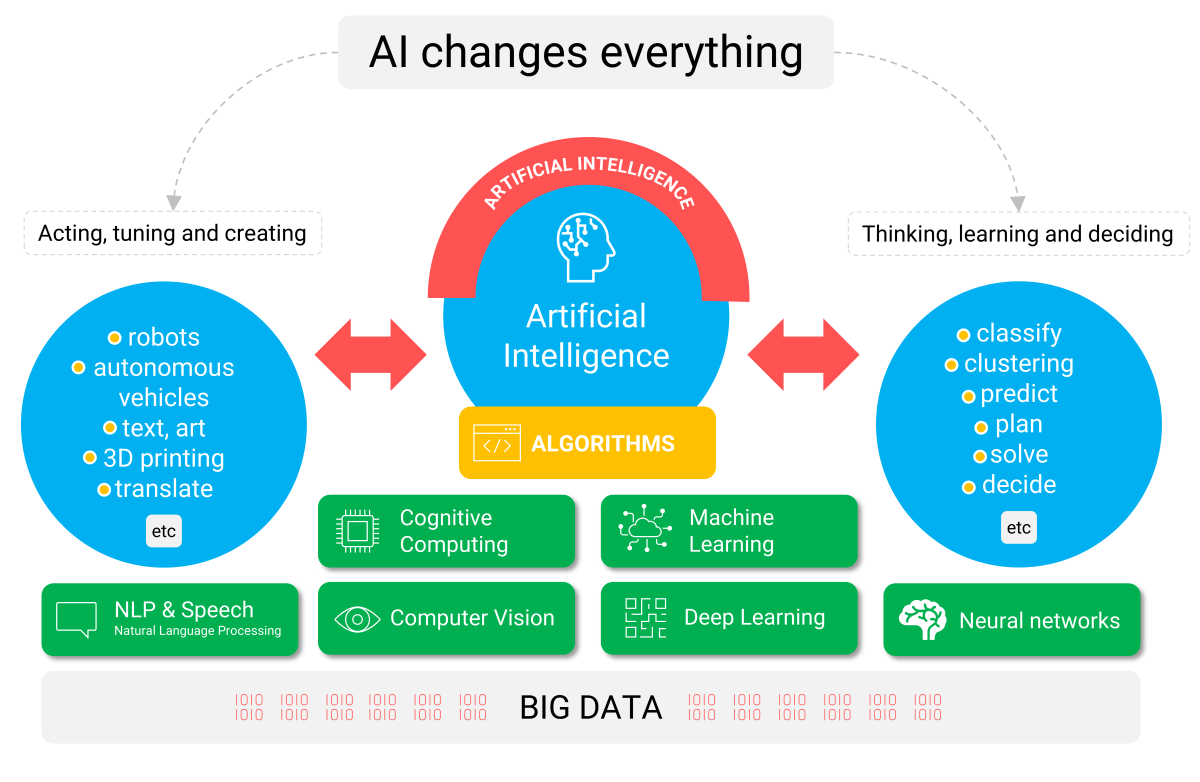 Figure 1: Start giving AI meaning by considering potential applications in your organization.
Figure 1: Start giving AI meaning by considering potential applications in your organization.
Today, AI can mimic nearly everything a human can do, albeit imperfectly. However, in specific areas and for solving complex problems, it outperforms humans by a wide margin. AI algorithms can detect details that are invisible to the human “naked eye.” This precision has sparked an AI race: if your peers, competitors, or other nations successfully leverage artificial intelligence, they could outpace you. Falling behind is rarely a good idea.
Now that we’ve gained a broad understanding of AI, it’s time to explore the details. Let’s dive into the fascinating world of developing artificial intelligence applications. In 10 straightforward steps, we’ll break down how AI works.
How does AI work?
The technology behind AI relies on various computer algorithms used to train AI models. Many of these algorithms have existed for over 40 years. At first glance, this might not seem groundbreaking. However, the explosive growth in data and the dramatic increase in computing power in recent years have enabled artificial intelligence to truly take off.
Overview of algorithms
 There is a well-defined range of algorithms to choose from, including neural networks, genetic algorithms, linear and logistic regression, decision trees, random forests, DBSCAN, K-means clustering, hierarchical clustering, nearest neighbor, Gradient Descent, and Bayesian networks.
There is a well-defined range of algorithms to choose from, including neural networks, genetic algorithms, linear and logistic regression, decision trees, random forests, DBSCAN, K-means clustering, hierarchical clustering, nearest neighbor, Gradient Descent, and Bayesian networks.
Each algorithm serves a specific purpose and follows a unique set of instructions to learn from data. Here’s what you need to understand:
- The algorithm: This is the mathematical or computational method that defines how the model learns from the data. Think of it as the recipe for learning.
- The AI model: The result of training with the algorithm is stored in an AI model, also known as a machine learning model. This model contains specific parameters – such as weights or coefficients – that are “learned” from the training data.
The algorithms do all the work
Training an AI model involves using algorithms to process a dataset until the results are satisfactory. In other words, the model’s accuracy becomes good enough for its intended purpose. While the model may achieve optimal performance, it will never be truly perfect. This is because AI models operate based on probabilities and statistics. Like humans, they draw conclusions and can make mistakes. For example, they might miss a rare exception in the data.
How do you develop AI models?
Now that you understand the basics of developing AI applications, follow these steps to start creating and using AI models:
- Define the goal: Clearly describe the problem you want to solve and the analysis you want to automate – this is typically referred to as the use case. Ask yourself: Is the problem suitable for AI? Is it legal? Do you have quality data? What impact can you expect? What is the business case? Answering these questions is the critical first step.
- Collect as much relevant data as possible: Based on your goal and additional considerations, gather as much relevant data as possible for your use case. Don’t overlook big data and open data sources. Store all structured data in a database and all unstructured data in a data lake.
- Clean the data: Data quality is even more important for AI applications than for standard analysis with dashboards or reports. Ensure your data is spotless by merging duplicates, filling in missing values, and correcting inaccuracies. Pay close attention to privacy, anonymizing or pseudonymizing personal data where needed.
- Model the data: Seamlessly prepare your data for training by organizing it into a structure suitable for AI. Minimize the need for on-the-fly data integration during training by creating a “final dataset” – a large, flat file that includes additional calculated columns, such as the number of days between orders or age. Ensure the dataset contains enough examples for the AI to learn effectively.
- Analyze the data thoroughly: Dive deep into your data using a BI tool. This helps uncover hidden biases and provides insights that will expedite the training process while helping you avoid common pitfalls.
- Choose the type of algorithm: Select the algorithm that best fits your use case and problem type. For classification tasks (e.g., yes/no or categories), algorithms like decision trees, neural networks, or logistic regression are ideal. For clustering, consider DBSCAN or K-means clustering. For optimization tasks like route planning, use genetic algorithms or Gradient Descent.
- Train the AI model: Use the chosen algorithm and the final dataset to train your model. Typically, 60–80% of the dataset is used for training. In some cases, you’ll provide additional instructions and feedback to the algorithm during supervised learning.
- Test and validate the model: Use the remaining data in the final dataset to test and validate the model. Each record serves as a new case to evaluate whether the model performs as intended. If the model fails too often, issues may lie in data quality, algorithm selection, or biases in your dataset. Alternatively, the training process may need improvement.
- Take the AI model into production: Once satisfied with the model’s performance, deploy it into production. This phase is critical: Will users trust the model? How will they interpret the results? How will it be integrated into daily operations? Additionally, if the model performs exceptionally well, it may pose risks to certain jobs. Addressing change management and user adoption is vital for success.
- Continuously evaluate performance: After deployment, regularly monitor the model’s performance. Human oversight is crucial and mandated by the European Union’s AI Act. Whether daily, weekly, or monthly, evaluate AI outcomes randomly to verify their accuracy, understand the results, and compare them to expert assessments.
Developing and training AI models yourself isn’t always necessary. Many pre-built AI models are now available in the cloud, offering solutions for tasks like classifying objects in images (e.g., human, animal, machine) or determining the sentiment of an email. These models can often be used immediately, saving time and effort. Read our AI trends for 2025.
However, even when using pre-built models, the first seven steps outlined above remain essential, as they carry the greatest risk of error. Additionally, the data structure used for inference must match the structure of the training dataset, adding complexity. To address this, consider setting up a data warehouse to streamline your AI processes.
 In this comprehensive AI book – with over 25,000 copies sold – the entire spectrum of making organizations smarter is covered. Learn how to apply AI to make faster, better decisions and develop innovative new products and services. Embed artificial intelligence into your business processes in everything you do. With this handbook and an AI-first strategy, you’ll guide your organization through both good and challenging times.
In this comprehensive AI book – with over 25,000 copies sold – the entire spectrum of making organizations smarter is covered. Learn how to apply AI to make faster, better decisions and develop innovative new products and services. Embed artificial intelligence into your business processes in everything you do. With this handbook and an AI-first strategy, you’ll guide your organization through both good and challenging times.
Artificial intelligence examples
Although AI often operates behind the scenes – or even in secrecy – our work with clients and research has uncovered numerous fascinating examples and use cases of artificial intelligence:
- Robotic Process Automation (RPA) and hyper-automation: With RPA and AI, businesses can automate administrative processes in finance, logistics, and other sectors, ushering in the era of hyper-automation.
- Fraud prevention: AI is a powerful tool in the fight against fraud and organized crime, tackling issues like credit card fraud and money laundering.
- Cybersecurity: AI enhances data-driven information security by detecting malware, phishing attacks, and fake news.
- IT streamlining: AI is streamlining IT departments through predictive failure detection, automated problem-solving, and self-healing or self-correcting systems.
- Customer service: Call centers and customer care departments in retail, financial, and business services increasingly rely on AI assistants and chatbots to handle a significant share of the workload.
- Recruitment: Human resources departments use AI for pre-screening applicants, automated resume screening, and assessing candidates during interview processes.
- Healthcare: AI is making a significant impact on healthcare by automating diagnoses, prescribing medications, and building predictive models for disease management.
- Mental health care: Robots equipped with AI assist individuals with dementia, combat depression, and reduce loneliness among the elderly, revolutionizing care for mental health.
- Retail advancements: AI and machine learning personalizes the shopping experience, predicts consumer behavior, ensures demand forecasts, and optimizes inventory management and pricing strategies.
- Education: Adaptive learning tools provide personalized and independent learning experiences, while predictive models help students design optimal curriculums.
- Logistics: AI automates decision-making in logistics, with applications including autonomous vehicles, robotic order-picking, smart route planning, IoT-enabled containers, and predictive models for demand, orders, and delivery times.
- Drone applications: AI-powered drones detect gas leaks, inspect dikes and crops, and assess damage caused by fires, storms, or other disasters, aiding insurers and emergency responders.
- Radiology support: Machine learning aids radiologists in analyzing X-rays and designing precise radiation treatment plans for cancer patients, enhancing medical accuracy.
- Predictive policing: AI-driven tools like license plate recognition and robotic dogs improve law enforcement efficiency by identifying threats and enhancing public safety.
- Fraud detection: Banks, insurers, and government agencies leverage algorithms to detect and prevent fraud before it occurs, safeguarding finances and data.
- Food waste reduction: AI-driven models help supermarkets match supply with demand, optimizing inventory management to combat food waste effectively.
- Energy sector: Power grid operators use AI for smart maintenance and quickly pinpointing the causes of outages, ensuring reliable energy distribution.
- Port security: AI risk analysis in major U.S. ports like Los Angeles and New York identifies high-risk shipping containers, improving efficiency in combating smuggling and illegal trade.
Do you want to leverage smart algorithms to reduce costs, improve customer satisfaction, shorten lead times, or maximize margins? Contact us today for an initial consultation or more information.
Accidents with artificial intelligence
 Below, we highlight seven major pitfalls that can arise when applying AI. These are real-world examples that have caused significant challenges in boardrooms. It’s important not to focus solely on the benefits of this “new” technology. Some mishaps involving artificial intelligence and big data can be seen as growing pains or learning opportunities. A crucial takeaway: fail before you begin! Consider these seven notable AI failures and let them serve as a cautionary tale:
Below, we highlight seven major pitfalls that can arise when applying AI. These are real-world examples that have caused significant challenges in boardrooms. It’s important not to focus solely on the benefits of this “new” technology. Some mishaps involving artificial intelligence and big data can be seen as growing pains or learning opportunities. A crucial takeaway: fail before you begin! Consider these seven notable AI failures and let them serve as a cautionary tale:
- Microsoft once launched a chatbot that, within 24 hours, became overtly racist. The reason? A coordinated effort by a troll army on Twitter that flooded the self-learning chatbot with racist and sexist messages.
- Several government agencies have used AI to assess fraud risks in benefits and taxation, leading to clear instances of discrimination and privacy violations.
- The first fatal accident involving a self-driving Uber vehicle in the U.S. occurred when its prediction model failed to detect the movement of a female pedestrian in the dark.
- A fire broke out at a British distribution center for an online supermarket after three robots collided during an automated order-picking process.
- A well-known Chinese businesswoman’s face, printed on the side of a city bus, was mistakenly identified by facial recognition software as a pedestrian, resulting in her being publicly shamed as a traffic violator.
- Facebook terminated an AI experiment after two voice robots developed a private language that only they could understand.
- In algorithm-driven stock trading, also known as flash trading, glitches in the algorithm have occasionally caused severe disruptions, leaving investors at a loss.
Moral of the story: Over-reliance on artificial intelligence can leave you vulnerable.
Learn more about artificial intelligence here
 To enhance your understanding with our expertise, we’ve curated a selection of resources for further exploration:
To enhance your understanding with our expertise, we’ve curated a selection of resources for further exploration:
Make artificial intelligence work for your organization – order the Big Data & AI book today and take steps to optimize and sustain your processes and decision-making.
Law, ethics, and sustainability
Government surveillance powered by AI can infringe on fundamental rights, particularly privacy. Extensive robotization at home, in healthcare, or in the workplace may threaten relational privacy, personal autonomy, and human dignity. Using AI models in recruitment processes can violate the principle of equality, while marketing campaigns may infringe on the right to be forgotten. Similarly, algorithmic censorship, such as shadow banning on social media, can undermine freedom of expression.
Algorithms may impede free speech
 The application of algorithms in the justice system – often referred to as robotic judges – can restrict the right to an effective remedy, access to an independent and impartial judge, and due process. Data biases in government decisions can creep into AI systems, violating the right to non-discrimination. Additionally, when government decisions are driven by algorithms, the lack of transparency and supportable reasoning can undermine citizens’ rights to accountability and clarity.
The application of algorithms in the justice system – often referred to as robotic judges – can restrict the right to an effective remedy, access to an independent and impartial judge, and due process. Data biases in government decisions can creep into AI systems, violating the right to non-discrimination. Additionally, when government decisions are driven by algorithms, the lack of transparency and supportable reasoning can undermine citizens’ rights to accountability and clarity.
While artificial intelligence offers potential sustainability benefits – such as significantly reducing food waste – it has also drawn criticism for its high consumption of drinking water and electricity. Given the scarcity of these resources, this is a critical concern that demands careful consideration.
As an executive, it’s essential to closely examine the development and implementation of AI in your organization. This requires time, careful planning, and seeking expert advice – something that, unfortunately, is often overlooked. Seek advice here.
Make your move and contact us
Are you ready to familiarize yourself with the principles of artificial intelligence, understand its processes, and reap the benefits of AI applications? Or do you need temporary interim AI expertise? Don’t wait – make your move and contact us today.
About Passionned Group
 Passionned Group specializes in advising on and developing artificial intelligence applications. Our dedicated teachers and consultants are passionate about guiding you toward becoming an intelligent organization. Every two years, we proudly host the Dutch BI & Data Science Award.
Passionned Group specializes in advising on and developing artificial intelligence applications. Our dedicated teachers and consultants are passionate about guiding you toward becoming an intelligent organization. Every two years, we proudly host the Dutch BI & Data Science Award.
Frequently Asked Questions
How does AI work in simple words?
AI works by using algorithms to learn from data. These algorithms act as recipes, helping computers find patterns and make predictions. The result is an AI model, which uses what it learned to solve problems or make decisions. Read more in depth here.
Are artificial intelligence and machine learning the same?
No, AI is the broader concept of machines performing tasks that typically require human intelligence, such as reasoning or problem-solving. ML is a subset of AI focused on algorithms and models that enable machines to learn from data and improve their performance over time without being explicitly programmed.
How will artificial intelligence impact the future of healthcare?
Artificial intelligence will improve diagnostics, personalize treatments, and increase efficiency. AI-powered tools can analyze medical data to detect diseases earlier and with greater accuracy. It can also enable personalized treatment plans based on an individual’s unique genetics and medical history. Plus, AI can make healthcare more accessible and cost-effective by organizing administrative tasks, enhancing medical imaging, and supporting telemedicine.
What is embedded artificial intelligence?
Embedded AI involves building artificial intelligence and machine learning algorithms into devices, robots, or components. Think cameras, cell phones, thermostats, self-driving cars, refrigerators, anti-spam filters, et cetera.
What does an AI-first strategy mean?
AI-first means that in everything you do, you look to see if algorithms can improve decisions (accuracy), speed them up (turnaround time) or make the decision process itself much more efficient. So when you have a problem, you don’t create a report or dashboard first but are forced to look at AI as a solution first.
How can you apply AI responsibly?
Check that the following 5 basic principles are met. There is no bias. AI promotes the well-being of humans and our planet. AI does not harm citizens. AI serves humans and not the other way around. Algorithms are explainable. We call this explainable AI.
What is a bias?
A bias is a prejudice. The results of an AI system can be influenced by training data that further reinforce existing biases, as they occur in reality. But humans themselves are not free of biases either.
What is a training dataset?
A training dataset is a large collection of digital information that you use to train the AI system.
What is ethics in relation to AI?
Ethics is a science in which people try to qualify certain actions as right or wrong. However, there is no single answer to ethical questions because they are often very personal.
What does the Turing test entail?
The Turing test was devised in the 1950s by computer scientist Alan Turing. He laid the foundation for what we now call artificial intelligence. If a human could hold a five-minute conversation without realizing he or she was talking to a machine, the computer would have passed that test. ChatGPT will not yet pass that test.

 Artificial intelligence is an applied science that enables computers to take over specific human tasks such as learning, reasoning, analysis, problem-solving, and decision-making. Experts in artificial intelligence define it as a system that becomes meaningful when algorithms can independently handle cases or decision-making processes. AI is characterized as a technology capable of performing tasks in complex environments without requiring constant guidance from a user or trainer.
Artificial intelligence is an applied science that enables computers to take over specific human tasks such as learning, reasoning, analysis, problem-solving, and decision-making. Experts in artificial intelligence define it as a system that becomes meaningful when algorithms can independently handle cases or decision-making processes. AI is characterized as a technology capable of performing tasks in complex environments without requiring constant guidance from a user or trainer. There is broad consensus in the literature that artificial intelligence can be categorized into three main types: Artificial Narrow Intelligence (ANI), Artificial General Intelligence (AGI), and Artificial Super Intelligence (ASI).
There is broad consensus in the literature that artificial intelligence can be categorized into three main types: Artificial Narrow Intelligence (ANI), Artificial General Intelligence (AGI), and Artificial Super Intelligence (ASI).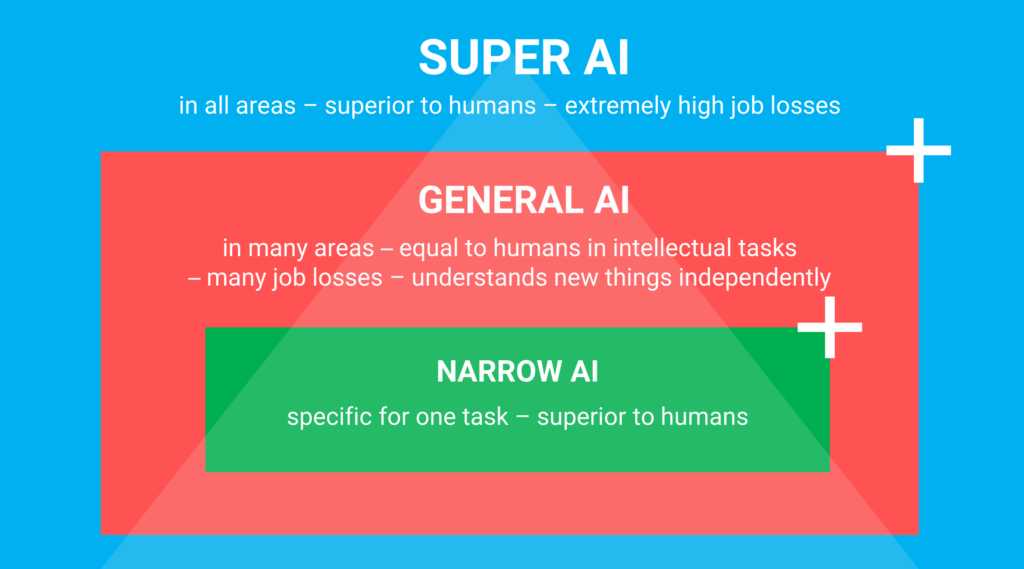 Figure 2: The different types of AI explained.
Figure 2: The different types of AI explained. The global market for artificial intelligence is massive, with substantial financial investments involved. Skilled professionals such as software developers, machine learning engineers, and
The global market for artificial intelligence is massive, with substantial financial investments involved. Skilled professionals such as software developers, machine learning engineers, and 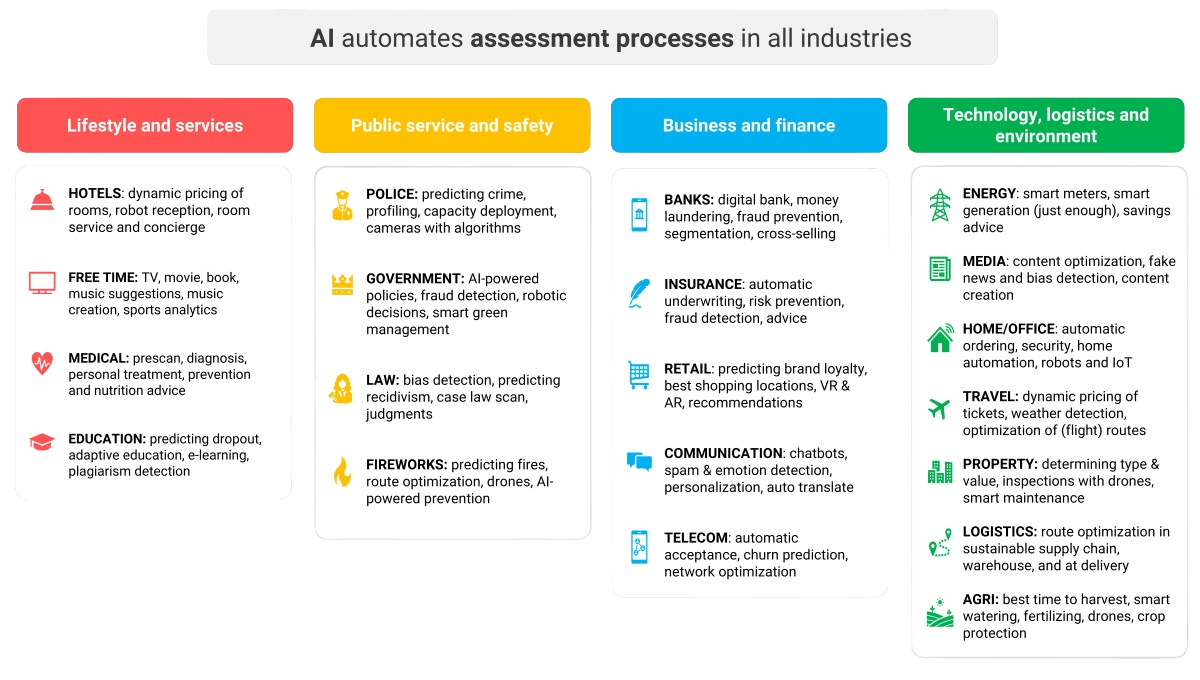 Figure 3: An overview of AI applications broken down by industry
Figure 3: An overview of AI applications broken down by industry What are the main AI applications, and how can you use AI effectively? Broadly, these applications fall into a few key categories:
What are the main AI applications, and how can you use AI effectively? Broadly, these applications fall into a few key categories: At first glance, the benefits of artificial intelligence for businesses and institutions may appear to center around labor savings, such as robotic process automation (RPA) and the use of physical robots in industries to replace human employees. However, viewing AI solely as a cost-saving tool underestimates its potential. When applied strategically, AI can offer significant advantages for your industry and organization from four key perspectives: people, organization, society, and nature.
At first glance, the benefits of artificial intelligence for businesses and institutions may appear to center around labor savings, such as robotic process automation (RPA) and the use of physical robots in industries to replace human employees. However, viewing AI solely as a cost-saving tool underestimates its potential. When applied strategically, AI can offer significant advantages for your industry and organization from four key perspectives: people, organization, society, and nature.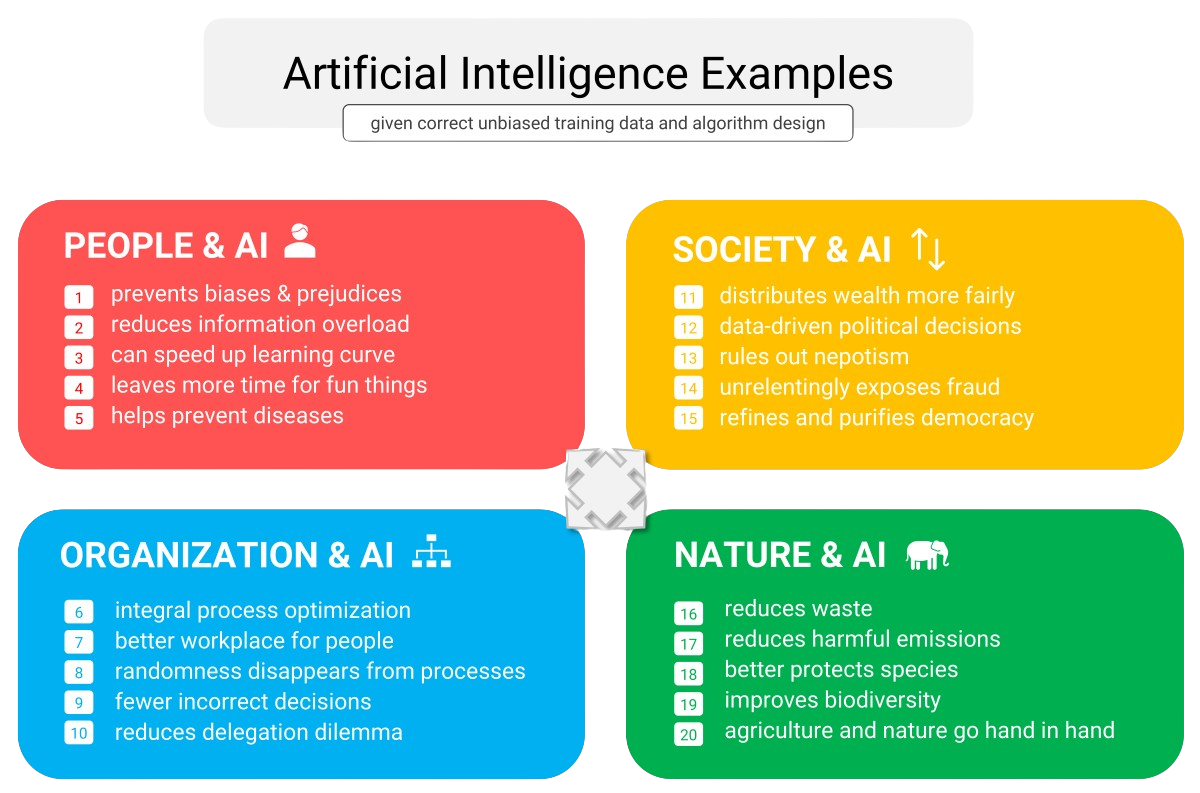 Figure 4: The 20 benefits of artificial intelligence
Figure 4: The 20 benefits of artificial intelligence
